A useful way of thinking about many climate problems is to boil them down to a few key variables. For example, the Equilibrium Climate Sensitivity (ECS) is a nice way of summarizing the climate impacts of doubling CO\(_2\) concentrations, as many aspects of the climate system’s response scale with global-mean surface temperature. Then if you want to constrain the ECS, you just have to understand two variables, the radiative forcing from doubling CO\(_2\) and the feedbacks which bring Earth’s energy imbalance back to equilibrium: $$ ECS = F / \lambda. $$ Uncertainty in ECS comes equally from uncertainty in \(F\) and from uncertainty in \(\lambda^{-1}\). Since the relative uncertainty in \(\lambda^{-1}\) is about three times the uncertainty in \(F\) (see the figure below), most of the focus is on better constraining climate feedbacks, like how low clouds change with warming.

But the experiment we’re running on the climate system is a transient experiment -- CO\(_2\) concentrations are going up every year. To quantify transient warming, people like to use the Transient Climate Response (TCR): the global-mean warming after 70 years of increasing CO\(_2\) concentrations by 1% per year (this produces a doubling after 70 years). The TCR might be more useful for thinking about how much warmer Earth will be at the end of the 21st century than the ECS, but it also involves a few more variables. These include the heat capacity of the combined land surface and ocean mixed layer (\(c\)), the rate of heat exchange between the ocean mixed-layer and the deep ocean (\(\gamma\)), the “efficacy” of ocean heat uptake (\(\epsilon\)) and the heat capacity of the deep ocean (\(c_0\)). These can all be combined into a two-box model of the climate system: $$ c\frac{dT_1(t)}{dt} = F(t) - \lambda T_1(t) - \epsilon\gamma(T_1(t) - T_2(t)), $$ $$ c_0\frac{dT_2(t)}{dt} = \gamma(T_1(t) - T_2(t)), $$ where \(T\) is the temperature of the upper layer and \(T_0\) is the temperature of the deep ocean. The efficacy accounts for the fact that 1Wm\(^{-2}\) of ocean heat uptake has a different warming effect than 1Wm\(^{-2}\) of forcing, and is usually \(> 1\). The TCR is the warming of \(T\) after 70 years of linearly increasing \(F\), and we now have six variables to think about: \(F\), \(\lambda\), \(c\), \(c_0\), \(\gamma\) and \(\epsilon\).

Max Popp and I recently wrote a GRL paper on "Probing the Sources of Uncertainty in Transient Warming on Different Time Scales", where we tried to understand how these variables combine to produce uncertainty in transient warming (i.e., in the TCR). I think our results are useful for thinking about how to reduce transient warming uncertainty, as well as for how to interpret the spread in ECS values in the CMIP6 models, which looks like it's going to be larger than for the CMIP5 models. In this post I’m going to summarize our main findings, and then in Part 2 I’ll give the nitty-gritty details of how we got there.

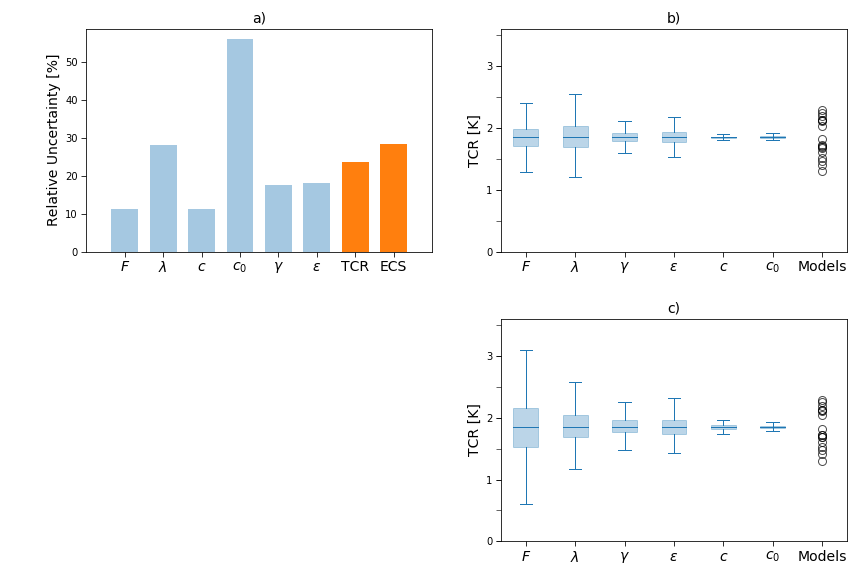
Figure 1 from the paper: a) The relative uncertainties (standard deviation across models divided by model mean) in the six parameters of the two-box model (blue bars), based on fitting 18 CMIP5 models, as well as the uncertainties in the ECS and the TCR (orange bars). b) Uncertainty in the TCR due to uncertainty in each parameter, holding the other paramters fixed. The circles show the actual model TCR values. c) Same as panel b) but the assuming the same relative uncertainty in each parameter.

Our main goal was to separate out (1) the uncertainty in each variable, from (2) the sensitivity of transient warming to uncertainty in each variable. A variable could be highly uncertain but contribute little to uncertainty in the TCR, or vice-versa: a variable could be well known, but still be responsible for a lot of uncertainty. To put it another way: there’s a lot of emphasis on constraining the net climate feedback, but maybe there’s a better way of reducing uncertainty in the TCR?

In fact, from a theoretical analysis of the two-box model and by looking at data from CMIP5 models, we found that the TCR (and transient warming generally) is actually most sensitive to uncertainty in the forcing. The climate feedback is much more uncertain than the forcing, making it the primary cause of uncertainty in the TCR, but if the radiative forcing from doubling CO\(_2\) was as uncertain as the feedback, the best guess for the TCR would be \(\sim\)0.5-3.5\(^\circ\)C, instead of 1-2.5\(^\circ\)C.

Another way of saying this is that reducing the uncertainty in \(F\) by 1% would reduce the uncertainty in the TCR much more than reducing the relative uncertainty in \(\lambda\) by 1%. Similarly, uncertainties in emissions, and in the carbon-cycle feedbacks which control how fast atmospheric CO\(_2\) concentrations rise, could overwhelm uncertainties in the feedbacks. A recent Science perspective showed that an easy way of reducing the intermodel spread in \(F\) is to only use radiative transfer parameterizations that have been thoroughly vetted against line-by-line calculations. Clearly, we should be doing this ASAP.

Somewhat more technically, we also showed that ocean heat uptake efficacy is responsible for more uncertainty than the rate of ocean heat uptake. Furthermore, the contribution of both of these to transient warming uncertainty peaks on time-scales of 15-20 years, and then declines on longer time-scales. So the ocean is less important than radiation and climate feedbacks, but it's still worth reducing the intermodel spread in the ocean-related variables. My favorite paper on constraining ocean heat uptake is Kostov et al (2014).

Finally, we discussed two other implications of our results. First, it's dangerous to extrapolate from short-lived climate perturbations, like volcanic eruptions, to long-lived perturbations like CO\(_2\) increases. The response to short-lived perturbations is mostly determined by the upper ocean heat capacity, \(c\), and by the radiative forcing, and doesn’t depend strongly on the value of \(\lambda\). So if you’re trying to fit a climate model to a volcanic eruption you’ll mostly be fitting the upper ocean heat-capacity and the volcanic forcing, and you probably won't learn much about the feedbacks.

The other implication is that the feedbacks of models that are 'tuned' in some way to the historical record are strongly influenced by historical forcing estimates. By 'tuning' we were referring to both cases in which model parameters are explicitly tweaked to better fit the 20th century temperature record and cases in which a particular model is deemed to be of low quality because it does not fit the record well.

We think this is an important point for thinking about the next generation of CMIP6 models. More and more climate models are including representations of the aerosol indirect effect (AIE), which can make their estimates of the historical aerosol forcing larger (i.e., more negative). Making the historical aerosol forcing larger requires models to have a larger ECS in order to match the historical record (since the combined CO\(_2\) + aerosol forcing is smaller). But including the AIE doesn't always make the historical aerosol forcing larger, so it's also possible to build a low-ECS model that includes the AIE.

In any case, a rough calculation that we did gave a 2:1 relationship between uncertainty in climate models' net radiative feedback and uncertainty in the historical forcing. So by including the AIE, the CMIP6 models are likely increasing the intermodel spread in the historical forcing, and hence in the net climate feedback and the ECS.

The results that have come out so far suggest that some CMIP6 models are running very warm, while others have low ECS values near 2\(^\circ\)C, and it will be interesting to see what their estimates of the historical forcing look like. This doesn’t mean that climate models are getting "worse" or even that the ECS is becoming more uncertain. The raw model range isn’t the best way of estimating Earth’s ECS. But it does highlight how important it is to better constrain the historical aerosol forcing (see here for more).