In a previous post, I described two classes of emergent constraints on climate sensitivity: temperature-based constraints and cloud-based constraints. Temperature-based emergent constraints compare warming rates in historical simulations with observed temperature trends, and rule out models which don’t reproduce the observed record well. Cloud-based emergent constraints look at relationships between cloud cover (or cloud radiative effects) and surface temperatures on monthly, annual, etc. time-scales, and correlate these relationships across models with climate sensitivity. The idea is that since most of the uncertainty in climate sensitivity comes from clouds, the response of clouds to internal variability should tell us something about how clouds respond to warming.

A cloud-based emergent constraint that I've played around with is a "regional" constraint, which uses local regression co-efficients (\(\alpha_{loc}\)) between net or SW CRE and surface temperatures, binned into 5° by 5° boxes (the size of the boxes doesn't really matter). That is, for a box \(i\), \(\alpha_{loc, i} = \delta \)net CRE \(/ \delta T_s\), estimated using monthly or annual-mean data. These local regression co-efficients, for each box, can then be correlated across models with the models' (global) climate sensitivities.

I like this approach for several reasons: it hones in on the most relevant regions for developing emergent constraints, and if there are multiple “hot-spot” regions then the climate sensitivity estimates produced by each region can be checked against the others, providing a consistency check. It would be exciting if distinct climate regimes, like the subtropical north Pacific and the Southern Ocean, gave similar estimates of ECS.

In CMIP5 this regional constraint works well, consistent with other cloud-based emergent constraints. The figure below shows \(r^2\) values for correlations across models between \(\alpha_{loc}\) and equilibrium climate sensitivity (ECS) for 18 CMIP5 models. The \(\alpha_{loc}\) values are estimated from historical simulations, and the top panel shows results using monthly data and the bottom panel shows results using annual-mean data.

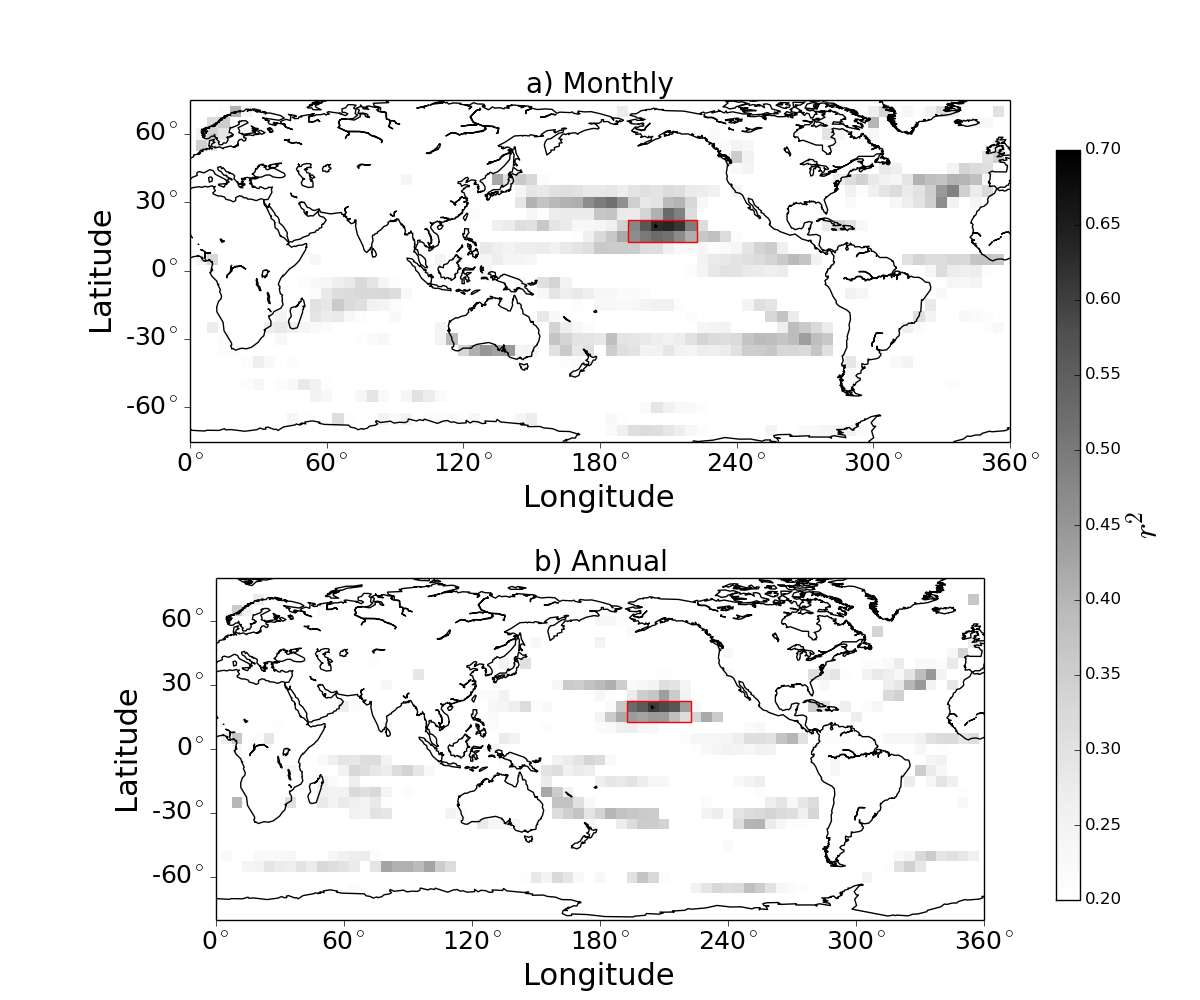
A number of "hot-spots" show-up, mostly on the edges of subtropical stratocumulus regions, with the most prominent hot-spot in the northeast Pacific, roughly centered over Hawaii. Combining surface temperatures from the ERA-Interim reanalysis and net CRE data from CERES, I have a rough emergent constraint on ECS based on the average value of monthly \(\alpha_{loc}\) in the region outlined by the red boxes.

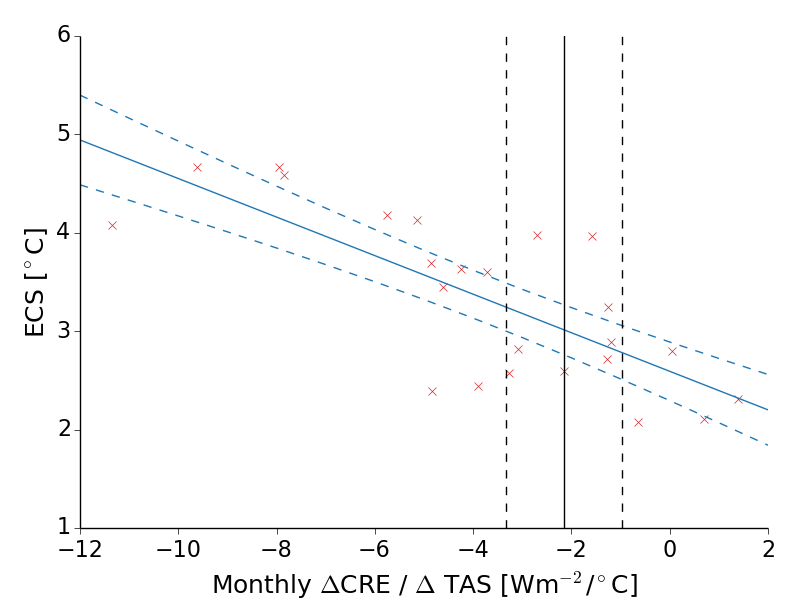
Interestingly, the ECS estimate is lower than most previous cloud-based emergent constraints, though this is a quick and dirty estimate. Nevertheless, so far the regional emergent constraint seems promising. But one of the criteria Caldwell et al. use to define a “credible” emergent constraint is that it holds in multiple ensembles. So how does the regional emergent constraint do in CMIP6? Not well…

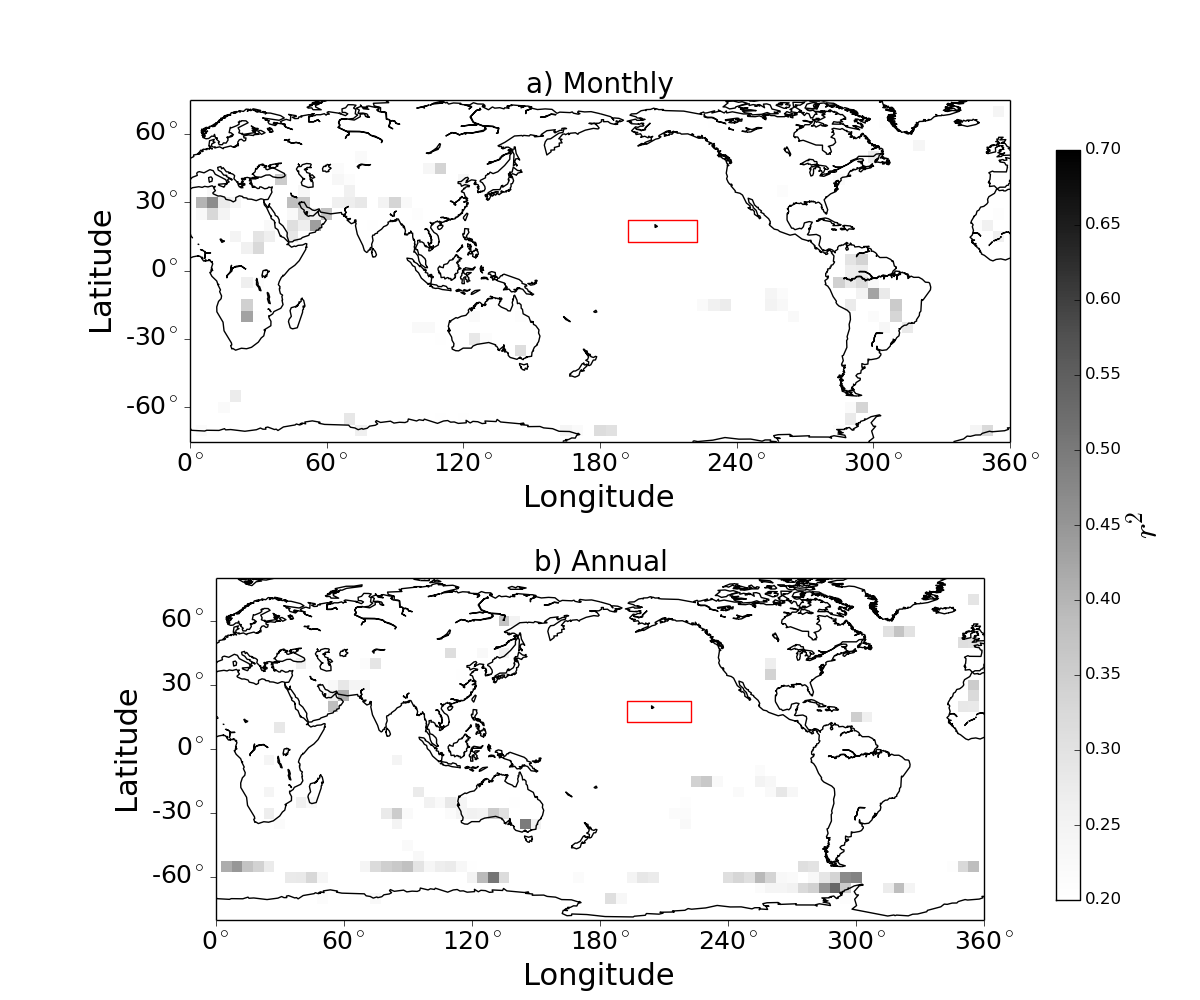
Apart from some hints in the Southern Ocean, there don’t seem to be any hot-spot regions in which local cloud fluctuations on monthly or annual time-scales tell us something about climate sensitivity. My guess is the other cloud-based constraints capture similar intermodel differences to the regional constraint, and also do worse in CMIP6 than in CMIP5.

Why wouldn’t cloud-based emergent constraints work in CMIP6? Zelinka et al. showed that (in the ensemble-mean) the high ECS values in CMIP6 are mostly due to large cloud feedbacks over the Southern Ocean. Whereas in CMIP5 (and also in CMIP3), most of the uncertainty in the cloud feedback came from subtropical descent regions. So one possibility is that CMIP6 has something like three classes of models: low sensitivity models, “CMIP5-like” models with high sensitivities driven by subtropical clouds, and a new set of high sensitivity models driven by Southern Ocean cloud feedbacks (see also this plot Mark posted on Twitter). Emergent constraints based on the variability of clouds in regions of subtropical descent would then fail, as would constraints based on Southern Ocean clouds. The only hope for a cloud-based emergent constraint would be if there were correlations between Southern Ocean clouds and subtropical clouds, or if we could rule out one group of high sensitivity models.

I don’t think this means the cloud-based emergent constraints that worked in CMIP5 are wrong, necessarily, but it does seem like it might be harder to develop this kind of emergent constraint for the CMIP6 models.

(Thanks to Joel Norris and Cristi Proistosescu for helpful conversations.)